Trao đổi khóa Diffie-Hellman
Nếu các bạn đã học và làm được 1 số bài tập từ mức trung bình trong phần RSA rồi (mong là vậy) thì chắc hẳn các bạn cũng biết thuật RSA hiện nay đang có nguy cơ bị máy tính lượng tử tiêu hủy trong tương lai. Điều đó xảy ra được là vì RSA bảo mật hay không thì phụ thuộc vào bài toán phân tích khóa, cụ thể hơn là phân tích thừa số nguyên tố.
Đối với Diffie-Hellman, vấn đề phân tích logarit rời rạc (Discrete Logarithm Problem) chính là mấu chốt. Trước khi đi vào quy trình hoạt động của giao thức trao đổi khóa này, ta sẽ tới phần toán liên quan tới trường hữu hạn, cụ thể là lý thuyết nhóm.
Lý thuyết nhóm
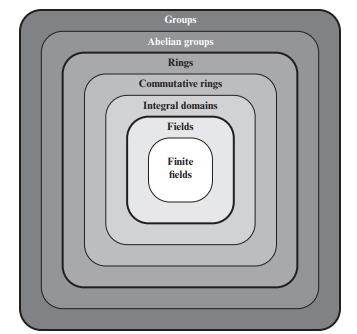
Nhóm, vành và trường là những yếu tố cơ bản của một nhánh toán học được gọi là đại số trừu tượng. Trong đại số trừu tượng, chúng ta không bị giới hạn bởi các phép toán số học thông thường. Sau đây là một số lý thuyết về nhóm mà bạn phải nắm để hiểu rõ bản chất của thuật toán:
Nhóm là một tập hợp, G, cùng với phép toán hai ngôi $\cdot$ (còn gọi là luật nhóm của G) kết hợp hai phần tử $a$ và $b$ bất kỳ để tạo ra một phần tử khác, viết là $a \cdot b$ hoặc $ab$. Để trở thành một nhóm, tập hợp và phép toán, $(G, \cdot)$, phải thỏa mãn bốn yêu cầu gọi là tiên đề nhóm:
- Tiên đề đóng (Closure): Với mọi $a, b$ thuộc $G$, kết quả của phép toán, $a \cdot b$, cũng thuộc G.
- Tính kết hợp (Associative): Với mọi $a, b, c \in G, (a \cdot b) \cdot c = a \cdot (b \cdot c)$.
- Phần tử đơn vị (Identity element): Tồn tại một phần tử $e$ trong $G$, sao cho đối với mỗi phần tử $a$ thuộc $G$, phương trình $e \cdot a = a \cdot e = a$ được thỏa mãn.
- Phần tử nghịch đảo (Inverse element): Đối với mỗi $a$ trong $G$, tồn tại một phần tử $b$ trong $G$ sao cho $a \cdot b = b \cdot a = e$, với $e$ là phần tử đơn vị.
Nếu một nhóm có số phần tử hữu hạn, nó được gọi là nhóm hữu hạn (ví dụ như nhóm cyclic $\mathbb{Z_n}$, nhóm đối xứng, nhóm hoán vị,…), và bậc của nhóm bằng số phần tử trong nhóm. Ngược lại, nhóm đó là nhóm vô hạn (ví dụ như nhóm số nguyên, nhóm số thực,…).
Đối với Diffie-Hellman, chúng ta sẽ làm việc nhiều với nhóm cyclic hữu hạn $\mathbb{Z_p^*}$ và phần tử sinh $g$ (Generator). Cụ thể hơn, nhóm cyclic là một nhóm được sinh ra từ một phần tử $g$ bằng cách áp dụng lặp đi lặp lại phép toán nhóm (ở DH thường là phép lũy thừa modulo p), phần tử này được gọi là phần tử sinh của nhóm.
Lúc nãy, mình có nhắc tới bậc mà chưa đề cập tới định nghĩa của nó thì đây:
Cho $G$ là một nhóm và $a \in G$ là một phần tử của nhóm. Giả sử tồn tại một số nguyên dương $d$ có tính chất $a^d = e$. Số $d$ nhỏ nhất như vậy được gọi là bậc của $a$. Nếu không tồn tại $d$ nào như vậy, thì $a$ được gọi là có bậc vô hạn.
Một số tính chất liên quan:
- Cho $G$ là một nhóm hữu hạn. Khi đó, mọi phần tử của $G$ đều có bậc hữu hạn. Hơn nữa, nếu $a \in G$ có bậc $d$ và nếu $a^k = e$, thì $d \ | \ k$.
- Định lý Lagrange: Cho $G$ là một nhóm hữu hạn và $a \in G$. Khi đó, bậc của $a$ chia hết bậc của $G$. Nghĩa là nếu $n = |G|$ là bậc của $G$ và $d$ là bậc của $a$. Khi đó: $a^n=e$ và $d \ | \ n$.
Trao đổi khóa Diffie-Hellman
Như đã nói, hiệu quả của thuật toán Diffie–Hellman phụ thuộc vào độ khó của việc tính toán logarit rời rạc. Để dẫn chứng minh họa thì mình đưa ra tấm hình sau đây vì a picture is worth a thousand words…
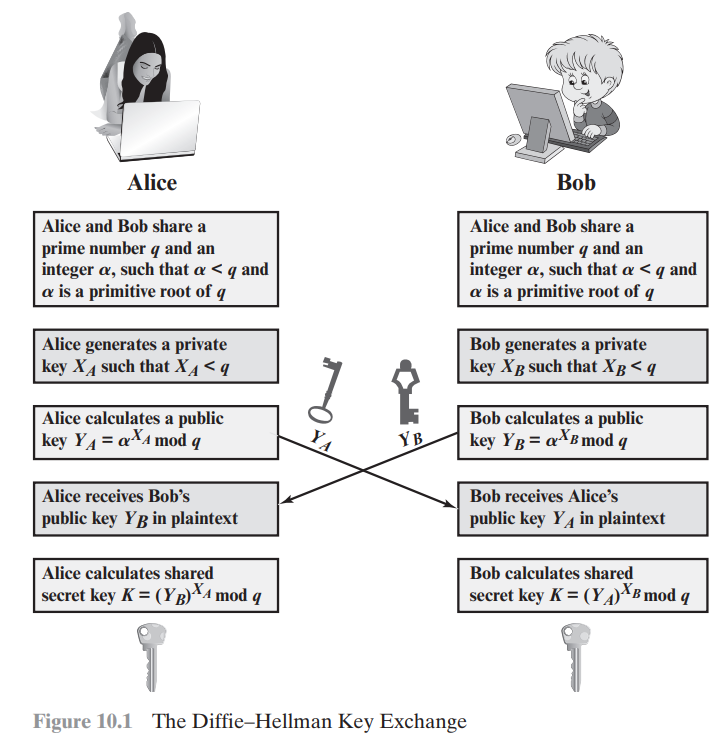
Ở đây, kết quả của hai bên nhận được là khóa chung vì:
$K_{\text{A}} = Y_B^{X_A} \pmod q=(\alpha^{X_B}\pmod q)^{X_A} \pmod q=(\alpha^{X_B})^{X_A}\pmod q=\alpha^{X_AX_B}\pmod q$
$K_{\text{B}} = Y_A^{X_B} \pmod q=(\alpha^{X_A}\pmod q)^{X_B} \pmod q=(\alpha^{X_A})^{X_B}\pmod q=\alpha^{X_AX_B}\pmod q$
Bây giờ, ví dụ ta đóng vai là người tấn công và muốn biết khóa chung này thì phải làm sao?
Vì $X_A, X_B$ là khóa riêng, ta chỉ có: $q, \alpha, Y_A, Y_B$. Do đó, ta buộc phải lấy logarit để tính khóa. Ví dụ để tính khóa riêng của B, ta tính: $X_B = \text{dlog}_{\alpha, q}(Y_B)$. Có được $X_B$, ta tính khóa chung $K = Y_A^{Y_B}\pmod q$
Rất khó để tính đúng không nào… Tuy vậy, muốn thì sẽ tìm cách, giao thức đơn giản trên vẫn không hề an toàn vì hoàn toàn có thể dính cuộc tấn công MITM (Man-in-the-Middle):
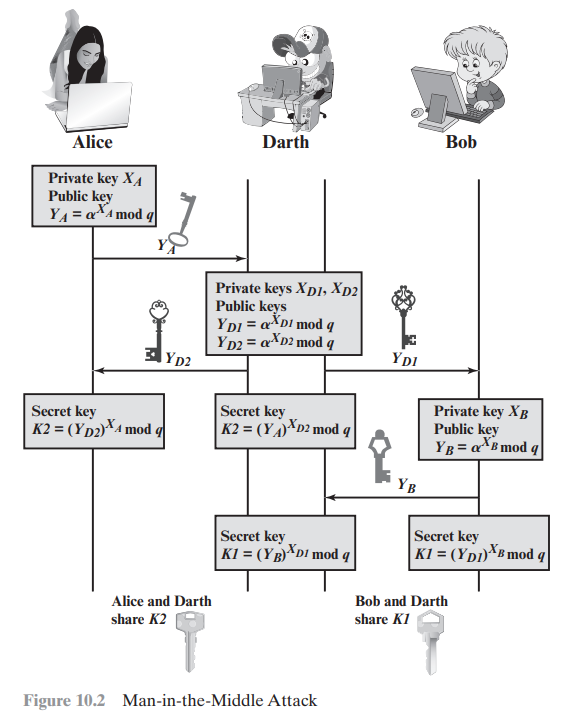
Người thứ ba khi đã can thiệp được vào cuộc trao đổi thì có thể tạo dữ liệu giả từ hai private key do họ tự làm ra và sử dụng nó để tạo khóa chung cho Alice và Bob, sau đó thì à không còn sau đó nữa dùng bộ khóa chung đó để mã hóa và giải mã tin nhắn rồi dùng nó làm chuyện tốt xấu thôi.
Đưa vào thực tế, ta có hệ thống mật mã Elgamal:

Về lý thuyết thì giao thức là vậy, trông thật vững chắc nhưng thực ra tất cả đều được cấu thành từ cái móng DLP và hiện tại thì ta có rất nhiều cách để tấn công nếu modulo có những tính chất đặc biệt:

Nhưng liệu có cách nào để ngăn chặn MITM trong phương pháp trao đổi khoá Diffie-Hellman hay không???
Câu trả lời là có. DH được sử dụng cho nhiều bộ mã hóa TLS 1.3 và cả TLS 1.2 và để nó ngăn được các cuộc tấn công MITM thì những giao thức này phải sử dụng mã hóa xác thực để đảm bảo tính toàn vẹn của dữ liệu. 1 số phương pháp mã hóa xác thực mà bạn có thể tham khảo tại đây.
Thế nếu muốn nâng cấp DH thì ta cần làm gì???
Để làm DH trở nên bảo mật hơn, ta phải nâng độ khó của DLP và đó là lúc ECC (Elliptic-curve cryptography) vào cuộc để sinh ra đứa con ECDH (Elliptic-curve Diffie–Hellman) nhưng bài viết đến đây cũng dài rồi nên hẹn bạn dịp sau :3
Bài tập
Sau đây là 1 số bài tập bắt buộc bạn cần làm để level up mớ kiến thức này vì practice makes perfect:
- CryptoHack phần Diffie-Hellman: Bắt buộc làm hết 3 phần Starter, Man In The Middle, Group Theory. Muốn trình cao thì làm thêm: phần MISC trong topic Diffie-Hellman luôn.
- Hackropole: Bắt buộc làm 2 bài El Gamal Fait 1/2 và 2/2.
- Dreamhack: Textbook-DH (Khuyến khích làm)
Tài liệu tham khảo
- Wikipedia: Định nghĩa của Nhóm, Cyclic group
- Cryptography and Network Security của William Stallings
- Chương 5.1: Groups - Finite Field
- Chương 10.1: Diffie-Hellman Key Exchange
- Chương 10.2: Elgamal Cryptographic System
- An Introduction to Mathematical Cryptography của Jeffrey Hoffstein, Jill Pipher, Joseph H. Silverman
- Chương 2.2: The Discrete Logarithm Problem
- Chương 2.3: Diffie–Hellman Key Exchange
- Chương 2.4: The Elgamal Public Key Cryptosystem
- Chương 2.5: An Overview of the Theory of Groups

