NSUCRYPTO 2025

In this article, I will provide guidance and the way how to solve some NSUCRYPTO 2025 problems using my own solutions.

Introduction

First and foremost, I want to send a huge thank you to everyone who supported me and helped me get to where I am today.

Round 1 was intense with 9 questions, including the infamous Question 4 that seemed impossible for everyone. To be honest, this year’s exam really threw me off. Even though I managed to tackle most of the problems, I walked away feeling unsure about the result.

But then, a miracle happened!!! I scored 24 points. Initially, I was awarded the Silver medal, but in a twist I didn’t see coming, about two hours later, that medal changed color to Gold! It was an absolute roller-coaster of emotions, and I couldn’t be happier.

Once again, thank you all so much!

Crypto growth

Description

One old, experienced cryptographer told his young student: You can’t live without this function. Really, I believe you’ll recognize it anywhere.

Do you?

Solution

The number in the picture is: 1 1 ? 2 ? 2 6 4 ? 4

It reminds me of Euler’s totient function. The numbers climbing the mountain in the puzzle correspond to the sequence of the function’s output for n = 1, 2, 3, 4, … and so on. 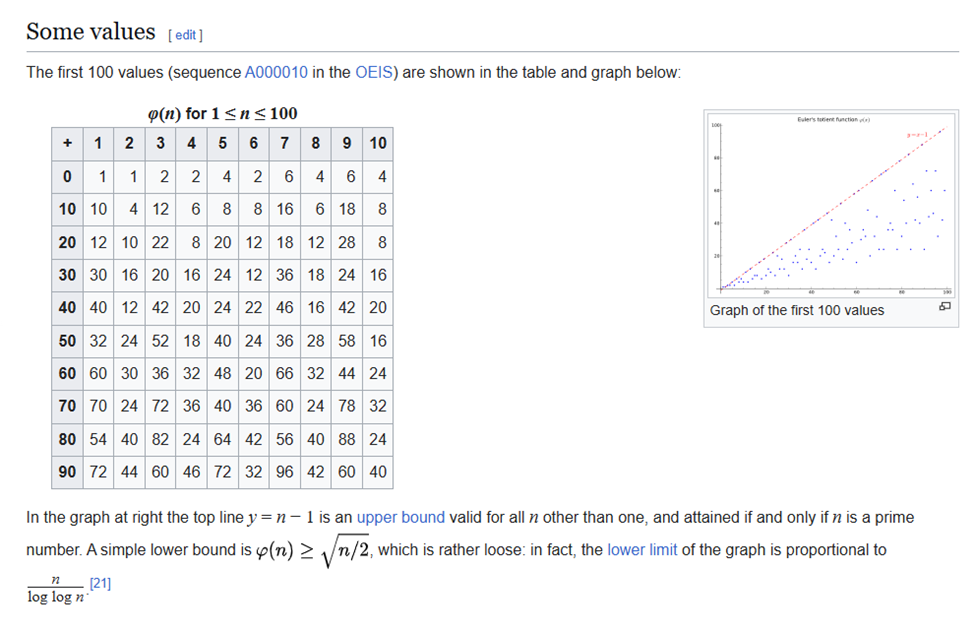So with the table, we have the result:

• The first ? is the 3rd term –> 2
• The second ? is the 5th term –> 4
• The third ? is the 9th term –> 6

Understand the Oracle

Description

Bob challenges Alice by providing a matrix $B \in \mathbb{Z}^{2n\times 2n}$ and asks her to find an integer vector $g \in \mathbb{Z}^{2n}$ that is short in the Euclidean norm and satisfies $Bf = g$, for some $f \in \mathbb{Z}^{2n}$.

Alice possesses a magical oracle capable of finding short vectors in dimension $n$, and it can be invoked any number of times. Bob further guarantees to Alice that there exists a way to reduce the dimension of $B$ to $n$, and that adding any two coefficients of the vector $g$ yields a small value. The first time, Bob challenged Alice by giving the matrix

Alice quickly realized that if she splits $g$ as $(g_0, g_1)$, then she can provide the oracle with the matrix $B_0 = H_0 + H_1$ of dimension $n$, such that $B_0(f_0 + f_1) = (g_0 + g_1)$ holds. Since $g_0 + g_1$ is still a short vector (by Bob’s guarantee), the oracle can find $g_0 + g_1$. Similarly, she can invoke the oracle with $B_1 = H_0 − H_1$ to obtain the vector $g_0 −g_1$, and ultimately recover $g$.

Bob then made the challenge harder and gave Alice a matrix of the form

where $H_0$ is a right circulant matrix and $H_1$ is a left-circulant matrix, and $H_0^T, H_1^T$ denote the transposes of $H_0$ and $H_1$, respectively. Can you help Alice to reduce this matrix to dimension $n$ so that she can use the oracle?

Note 1: We say that $H_0$ is a right circulant matrix if it has the form $\begin{pmatrix} a_0 & a_1 & \ldots & a_{n-1} \\ a_{n-1} & a_0 & \ldots & a_{n-2} \\ \vdots & \vdots & \ddots & \vdots \\ a_1 & a_2 & \ldots & a_0 \end{pmatrix}$, and similarly $H_1$ is a left circulant matrix if it has the form $\begin{pmatrix} b_0 & b_1 & \ldots & b_{n-1} \\ b_1 & b_2 & \ldots & b_0 \\ \vdots & \vdots & \ddots & \vdots \\ b_{n-1} & b_0 & \ldots & b_{n-2} \end{pmatrix}$.

Note 2: This problem is related to lattice-based cryptography, as finding the short vector $g$ corresponds to solving the Shortest Vector Problem (SVP) in the lattice generated by $B$.

Solution

This problem took up the most time, about two-thirds of the time. Luckily, it was worth it.

We use a special matrix known as the reversal matrix, denoted by $J$. The reversal matrix $J$ is an anti-diagonal identity matrix. It has two crucial properties:

1. It is its own inverse: $J^2=I$ (where $I$ is the identity matrix).
2. It can be used to relate the circulant matrices and their transposes. For a right-circulant matrix $H_0$ and a left-circulant (and symmetric) matrix $H_1$ as defined in the problem, we have:
   • $H_0^T=JH_0 J$
   • $H_1 J=JH_1$ (it commutes with $J$)

Set $f=(f_0,f_1),g=(g_0,g_1)$, then:

This gives two equations:

1. $H_0 f_0+H_1 f_1=g_0 \ \ \ (1)$
2. $H_1^T f_0+H_0^T f_1=g_1 \Leftrightarrow H_1 f_0+H_0^T f_1=g_1$ (because $H_1$ is a left-circulant matrix)

Subtitute $H_0^T=JH_0J$ into the second equation:

Add equation (1) to equation (3):

Subtract equation (3) from equation (1):

As you can see, Alice has successfully created two independent problems of dimension $n$.

• First Oracle Call:

  • She defines the matrix $B_+=H_0+H_1 J$.
  • She calculates the target short vector $g_+=g_0+Jg_1$.
  • She gives $B_+$ to the oracle. The oracle will return the short vector $f_+=f_0+Jf_1$.

• Second Oracle Call:

  • She defines the matrix $B_-=H_0-H_1 J$.
  • She calculates the target short vector $g_-=g_0-Jg_1$.
  • She gives $B_-$ to the oracle. The oracle will return the short vector $f_-=f_0-Jf_1$.

Then Alice can compute $f_0,f_1$ with two vectors $f_+,f_-$ from the oracle:

And this is the solution to Bob’s challenge: $f=(f_0,f_1)$

Key for the 2025

Description

The cipher key is defined by the positive integers $a, b, c, d, e, f, g, h, i$, such that the following relation holds:

Please, find the key!

Solution

I cherish the time I spent studying advanced mathematics in high school, which allowed me to immediately relate the knowledge to solve this problem.

We have the formula to calculate the sum of cubes of the first n positive integers:

With $n = 9$:

It seem to be related to the question, so we assume that the required numbers $a,b,\cdots,i$ have a relationship with the numbers $1,2,\cdots,9$. Let:

Substitute these values into the original equation:

From there, we have a set of valid solutions:

Negotiations (No solution yet)

Password to coins

Description

A famous Roman found a wallet with coins during his morning walk. To open it, he needs to enter a password hidden in the following line: 5655555556f012346789abcde5f012346789abcde5f012346789abcde5f012346789abcde5555555558d6ac5b6c8c8bec8b8c7cec5c9b4b3c8cab8c7cec5c9b47657f60718293a4bcde56789abcde5f01234f60718293a4bcde56789abcde5f012344444444456f57a7b55555555556ecbfe699badb4c3aaff8e4529b553cd616e459a11057a82ddf155555555

Help Julius to get the password and take 5 coins from the wallet.

Solution

This photo and this famous Roman coin reminds me of Julius Caesar, who invented the Caesar cipher. I believe the 5 coins mean that the key in the cipher is 5. So that, I wrote a script in Python to find the password:

s = """
5655555556f012346789abcde5f012346789abcde5f012346789abcde5f012346789
abcde5555555558d6ac5b6c8c8bec8b8c7cec5c9b4b3c8cab8c7cec5c9b47657f607
18293a4bcde56789abcde5f01234f60718293a4bcde56789abcde5f0123444444444
56f57a7b55555555556ecbfe699badb4c3aaff8e4529b553cd616e459a11057a82ddf
155555555
"""
lst = []
pt = ""
for i in s:
    try:
        k = (int(i, 16) - 5) % 16
        pt += format(k, 'x')
    except ValueError:
        if pt:
            lst.append(pt)
        pt = ""
for i in lst:
    try:
        print(bytes.fromhex(i))
    except ValueError:
        continue

And this is the result:

b'\x01\x00\x00\x00\x01\xab\xcd\xef\x124Vx\x90\xab\xcd\xef\x124Vx\x90\xab\xcd\xef\x124Vx\x90\xab\xcd\xef\x124'
b'Vx\x90\x00\x00\x00\x008\x15passiscryptonsucrypto!\x02\xa1\xb2'
b'\xc3\xd4\xe5\xf6x\x90\x124Vx\x90\xab\xcd\xef\xa1\xb2\xc3\xd4\xe5\xf6x\x90\x124Vx\x90\xab\xcd\xef\xff\xff\xff\xff'

On the second line I see ‘passis’ and know exactly what the key is: cryptonsucrypto!

A Greek cipher

Description

To encrypt the three-letter message we did the following. We matched each letter with it’s numeric equivalent according to the table, and got $p_1, p_2, p_3$. 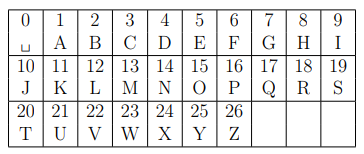Then we chose secret natural number δ and formed $p_4 = p_1 + p_2 + p_3 + \delta$.

After that we chose another secret natural number $\alpha$ and calculated for $i = 1, 2, 3, 4$

As a result we have got: WGAD. Recover the secret message.

Solution

I still don’t understand why I only got half the points for this question haha, maybe I’ll wait for the organizers’ explanation.

When I see the number of letter, I realize that it’s just have 27 character. Therefore, I try brute-force to find the right message. But in the first time, when I brute all $p_1,p_2,p_3,\delta,\alpha$ in range 27, it give me too much valid message. So I try to find more hint in the picture.

Then I see the picture, it can be the product: $\alpha \times \delta = 700$. Therefore, I add it in my code and compute exactly the message:

def solve_cipher():
    num_to_char = {
         0: " ",  1: "A",  2: "B",  3: "C",  4: "D",
         5: "E",  6: "F",  7: "G",  8: "H",  9: "I",
        10: "J", 11: "K", 12: "L", 13: "M", 14: "N",
        15: "O", 16: "P", 17: "Q", 18: "R", 19: "S",
        20: "T", 21: "U", 22: "V", 23: "W", 24: "X",
        25: "Y", 26: "Z",
    }

    char_to_num = {v: k for k, v in num_to_char.items()}

    c1 = char_to_num["W"]
    c2 = char_to_num["G"]
    c3 = char_to_num["A"]
    c4 = char_to_num["D"]

    for p1 in range(27):
        for p2 in range(27):
            for p3 in range(27):
                for delta in range(1, 27):
                    alpha = 700 // delta
                    if alpha * delta != 700:
                        continue
                    
                    p4 = p1 + p2 + p3 + delta

                    if (p1 + 2 * p2 - delta) % 27 != c1:
                        continue

                    if (p1 + p2 - alpha) % 27 != c2:
                        continue

                    if (p3 + 2 * p4 + delta) % 27 != c3:
                        continue

                    if (p3 + p4 + alpha) % 27 != c4:
                        continue

                    if alpha * delta != 700:
                        continue
                    
                    message = num_to_char[p1] + num_to_char[p2] + num_to_char[p3]
                    print(message)

if __name__ == "__main__":
    solve_cipher()

My answer for this problem is: VDC

Toy cipher cryptanalyst (Not having good solution, will be updated in the future)

Bijections for ciphers (Not having good solution, will be updated in the future)

Crypto noise

Description

Bob obtained from Alice the ciphertext $c = (c_1, c_2,\cdots, c_{20})$ that is a vector over $\mathbb{Z}_{16}$. He knows that the initial message is a vector $m = (m_1, m_2, m_3, m_4)$ over $\mathbb{Z}_{16}$. He also provided the information that for the ciphertext it holds

$c = mA + e \pmod {16}$ where A is a $4\times 20$ integer matrix

and $e = (e_1, e_2,\cdots, e_{20})$ is an unknown noise vector with elements from the set $\{−1, 0, +1\}$.

Let $c = (4, 2, 15, 11, 7, 4, 9, 5, 7, 2, 9, 4, 2, 14, 14, 13, 0, 8, 4, 12)$ and $\displaystyle \sum_{i=1}^{20}e_i^2=14$, provide the most efficient way to restore the initial message $m$ (or any possible candidates for it).

Remark. The points for the solutions obtained via brute force or any computer algebra systems will be reduced.

Solution

In this problem, my method is still not the most efficient way to restore $m$, which is LLL and the Nearest Plane algorithms.

Our original equation is:

Now, consider the set of all possible vectors that can be generated by multiplying an integer vector $m$ by the matrix $A$. This set forms a mathematical structure called a Lattice, denoted by $L$,

Because the problem states that $e$ has very small components (-1, 0, 1), it means that our target vector $c$ lies very close to some point on the lattice.

This is the exact definition of the Closest Vector Problem (CVP). Here is the mathematical method for solving CVP:

• Step 1: Lattice Basis Reduction

A single lattice can be described by many different sets of basis vectors. Solving CVP is much easier with a “good” basis (consisting of short, nearly orthogonal vectors).

By applying the LLL algorithm to the basis vectors of our lattice (the rows of $A$), we would obtain a new, “better” basis matrix $B$ that still generates the exact same lattice.

• Step 2: Babai’s Nearest Plane Algorithm

After we have a good basis $B$ from the LLL algorithm, we can use Babai’s Nearest Plane Algorithm to find the lattice point closest to our target vector. The idea behind it:

1. Express the target vector c as a linear combination of the new basis vectors: $c=\lambda_1 b_1+\lambda_2 b_2+\cdots$ (where the coefficients are real numbers).
2. Round each coefficient $\lambda_i$ to the nearest integer, let’s call them $k_i$.
3. The resulting lattice point $v=k_1 b_1+k_2 b_2+\cdots$ is an excellent candidate for the closest lattice point to $c$.

When the basis is sufficiently “good” and the noise vector e is sufficiently small, this algorithm has a very high probability of finding the exact closest lattice point.

Here is my script:

from sage.all import *
from itertools import combinations, product

A = Matrix(Zmod(16), [
 [2,2,1,1, -1, 0, 3, 7, -2, -2, -1, -1, -2, -2, -1, -1, -2, -2, -1, -1],
 [2,1,2,1, -2,-1,-2,-1, -1, 1, 2, 7, -2, -1, -2, -1, -2, -1, -2, -1],
 [1,2,1,2, -1,-2,-1,-2, -1,-2,-1,-2, 0, 0, 3, 6, -1, -2, -1, -2],
 [1,1,2,2, -1,-1,-2,-2, -1,-1,-2,-2, -1,-1,-2,-2, 0, 1, 2, 6]
])

c = vector(Zmod(16), [4,2,15,11,7,4,9,5,7,2,9,4,2,14,14,13,0,8,4,12])

def rep16(x):
    x = int(x)
    return x-16 if x>=8 else x

solutions = {}

for cols in combinations(range(20), 4):
    Asub = A.matrix_from_columns(cols)

    try:
        invA = Asub.inverse()
    except:
        continue
    
    csub = vector(Zmod(16), [c[i] for i in cols])

    for g in product([-1,0,1], repeat=4):
        rhs = csub - vector(Zmod(16), g)
        m = rhs * invA
        mA = m * A
        e = [rep16(c[j] - mA[j]) for j in range(20)]
        
        if all(x in (-1,0,1) for x in e) and sum(x*x for x in e) == 14:
            solutions[tuple(int(x) for x in m)] = (m, e, cols, g)
            
for m, _, _, _ in solutions.values():
    print("m =", [int(x) for x in m])

After using this method, I got the answer: m = [10, 10, 7, 5]